数学科

環論と代数幾何学

神田　遼

　数学は代数学、幾何学、解析学などの分野で分けられることが多いですが、これらの分野を結ぶ理論はたくさんあります。ここでは代数学と幾何学の間の関係の一例として、環論と代数幾何学の結び付きをご紹介します。

　環論は文字通り環という概念についての理論です。2つの整数の和と積は整数であり、結合法則や分配法則といったいくつかの性質を満たします。このように和・積の2つの演算を持つ集合で、 しかるべき性質を満たすものが環と呼ばれます。 整数全体の集合の他にも、有理数全体、実数全体、複素数全体の集合、さらには多項式全体の集合や（実数変数・実数値）関数全体の集合、n×n行列全体の集合などにも自然な和と積が定義され、環の構造を持ちます。

　一方、代数幾何学は多項式の零点集合（より正確には、いくつかの多項式の共通零点の集合）として定義される図形である代数多様体、およびその一般化を研究する学問です。 例えばx²+y²-1という2変数多項式を考えると、その零点集合はxy平面においてx²+y²-1=0を満たす集合であり、つまりこれは原点を中心とする半径1の円周です。 この円周を定義域に持つ関数のうち、正則関数と呼ばれる関数の全体をRとおくと、このRは環になります。 そして実は、この環Rの代数的情報だけから、元の円周を本質的に復元することができます。 こうして円周という幾何的対象は、環Rという代数的対象と対応し、円周の様々な幾何的性質がRの代数的性質と結び付きます。 例えば、空間において次元というのは基本的な不変量ですが、環に対しても、代数的に定義されるクルル次元という概念があり、円周の次元が1であるという事実は、対応する環Rのクルル次元が1であるという事実と対応します。 こうした考え方に基づき、古典的な代数多様体の概念をはるかに一般化して構築されたのが、グロタンディークによるスキームの理論であり、これは現代的な代数幾何学の基礎理論として扱われています。

　さて、実数という概念を用いて実ベクトル空間が、複素数という概念を用いて複素ベクトル空間が定義されますが、一般の環や代数多様体に対しても同様の概念が定義でき、それは環上の加群、代数多様体上の連接層と呼ばれます。1つの環（代数多様体）に対して、その加群（連接層）全体の集まりは圏と呼ばれる構造を持ちますが、このような圏を考えることで、一見異なる対象同士の深い結び付きが明らかになります。 例えば、n次元射影空間の連接層の圏は、ベイリンソン代数と呼ばれる環の（有限生成）加群の圏と導来同値であるというベイリンソンの定理がその代表例として知られています。

　環上の加群の圏や、その一般化であるアーベル圏が私の主な研究対象であり、特に、代数多様体やスキームの幾何的な情報が、その連接層の圏に反映される現象に興味を持っています。 例えば、ネーター性という性質を持つスキームに対して、その中に含まれる空間（閉部分スキーム）が、対応する圏の一部分（準連接層の圏の閉部分圏）と1対1に対応するという定理が知られていましたが、私はこれを、局所的にしかネーター性を持たないようなスキームに対して一般化しました。このような圏の研究では新しい理論が次々に現れており、今後の発展が楽しみです。

物理学科

量子楕円渦の発見：自発的対称性の破れの新展開

竹内 宏光

　この記事では最近の実験観測をきっかけにして理論的に導き出された自発的対称性の破れ（SSB: Spontaneous Symmetry Breaking）に関する研究の新たな展開を、筆者の最近の研究[1]（ネマチック・スピン秩序を有するボース・アインシュタイン凝縮体中の量子楕円渦）に基づいて紹介します。

　本学名誉教授の南部陽一郎先生がノーベル物理学賞を受賞された研究では、物性物理の超伝導現象を説明するSSBの概念が素粒子物理に応用されました。この事実に裏打ちされるように、SSBは素粒子・原子核・宇宙物理から物性物理に至るまで、あらゆる物理系に適用される普遍概念です。SSBが起こった物理系の性質を記述する際には「場」と呼ばれる時間と空間に依存した関数が共通して用いられます。つまりは場の運動を計算することができればその系の挙動を予測できるわけです。ところが場の自由度は無限大であるためその計算は一般に困難です。

　場の複雑な運動を記述する上で有効な方法があります。それは位相欠陥と呼ばれる場の中を漂う物体にその自由度を代表させるというやり方です。位相欠陥の「芯」の周辺では場はある決まった構造をとります。そのため芯の中心を質点の運動のように記述することで場の運動も近似的に予測できます。この状況はちょうど台風の目の進路を見れば今後の風向きの変化をある程度予測できることに似ています。超伝導体と超流体といったSSBが起こる典型的な物質では、この「風」は抵抗なしの電流と摩擦なしの流れに対応しています。対称性の破れ方に応じて芯の周りの場の構造は予測できるので、対称性の破れ方を大局的に把握していれば位相欠陥の挙動、すなわち場の挙動もよく理解できると考えられてきました。

　このような予測を否定する現象がソウル国立大学のShin教授の実験グループによって最近観測されました[2]。この実験系の対称性の破れ方は良く知られる通常の超伝導体・超流体と同様であるため、そこで現れる量子渦と呼ばれる位相欠陥の芯の形状は台風の目のように丸い点状になると予測されます。ところが実際に観測された位相欠陥は線状のものだったのです。図１は相転移を急に引き起こすことで生じた位相欠陥を実験で撮影した写真です。当時この位相欠陥は既知の２種類の位相欠陥が複合したもの（複合欠陥）とされ、臨界点近傍の相転移過程で一時的に起こる過渡的な状態だと解釈されました。

　もっと根本的に異常な状態が実現することが筆者による理論解析によってごく最近明らかにされました[1]。写真では線状の芯が容器の端から伸びて中央で途切れた構造をとっていますが、[1]によると最もエネルギー的に安定な状態は両端を持つ線分状の芯構造です。奇妙なことに流れは線分を迂回するように楕円に沿った構造をとります（図２右）。この事実は位相欠陥の運動がもはや質点のように扱える回転対称な渦としてではなく、楕円渦として線分のように扱わなければならないことを示唆しています。この異常な現象には芯の内部におけるSSBが深く関与していることがわかっています。SSBの研究は古くから行われていますが、芯内部の局所的なSSBがどのように起こるのか、またそれが位相欠陥の挙動にどのように影響するのかについて一般的な理解は得られていません。

　位相欠陥は超伝導体のような特殊な物質中だけでなく結晶や液晶といった馴染みのある系からスピントロニクスといった最先端の科学技術に至る様々な物性系で顔を出し、はたまた初期宇宙の相転移や高速回転する中性子星の内部運動でも重要な役割を果たすと考えられています。今後も上記発見のようなSSBに関する新たな展開が実験技術の向上とそれに応じた理論の進展によりもたらされ、物理分野全体に波及することを期待しています。

参考文献
[1] H. Takeuchi, Quantum elliptic vortex in a nematic-spin Bose-Einstein condensate, Phys. Rev.
　　Lett. 126, 195302, 2021.
[2] S. Kang, Sang W. Seo, H. Takeuchi, and Y Shin, Observation of wall-vortex composite defects
　　in a spinor Bose-Einstein condensate, Phys. Rev. Lett. 122, 095301, 2019.

化学科

微小反応場の化学

迫田 憲治

　多くの化学反応は溶液のなかで生じます。ここで、実際に実験で用いる溶液の量に注目してみますと、多くの場合、目に見える量の溶液（例えば 数十 mL とか）を使って実験をしています。一方、もし、溶液の量をものすごく少なくしたら、例えば、0.00000000001 mL にしたら、目に見える量の溶液のときと同じような化学反応が生じるのでしょうか。じつは、少なくとも直径が10ミクロンくらいよりも小さな液滴（微小液滴）では、化学反応の様子がかなり異なることが分かってきました。例えば、目に見える量の溶液（バルク溶液と言います）と比べて、微小液滴では化学反応が速く進んだり、バルク溶液とは異なる反応選択性を示したりする例が世界中から続々と報告されています。

　それでは、なぜ微小液滴ではバルク溶液とは異なる反応が進むのでしょうか。この原因についてはまだはっきりと分かっていません。私たちはこの原因を物理化学的な観点から明らかにしたいと考えて研究を進めています。特に私たちは、微小液滴内の化学反応を調べるために、単一の微小液滴を安定に空間捕捉し、この液滴をレーザー顕微鏡で詳しく観察するための装置を独自に開発しています（図１）。

　安定に空間捕捉された単一の微小液滴に光を照射すると、その光が液滴のなかに閉じ込められる、という現象が生じます。これは微小液滴が光共振器（合わせ鏡のようなもの）として振る舞うためです。微小液滴が光共振器として振る舞う性質を上手く利用すれば、液滴内部に溶存している分子の振る舞いを詳しく調べられることが私たちの研究で分かってきました。どうやら微小液滴のなかでは、分子がある特定の方向を向いており、これが微小液滴とバルク溶液での化学反応の違いを生み出す主要な原因の一つではないか、ということが明らかになってきました。

　微小液滴とバルク溶液では化学反応の特徴が大きく異なるわけですから、微小液滴のなかでの化学反応を詳しく研究していけば、これまで普通の体積をもった溶液の中では作ることができなかった化学物質を合成できるようになるかもしれません。また、生命現象の基本単位は細胞であり、細胞の中では莫大な数の化学反応が生じています。細胞というのは、水がつまったミクロンスケールの袋なわけですから、もしかしたら試験管のなかでの生化学反応と細胞中での生化学反応は異なる振る舞いを示すかもしれません。微小液滴の化学はそんなことを想像させるほど、ワクワクする現象を私たちに示してくれています。

生物学科

魚類の知性を研究する

幸田 正典

　長い間、哲学や心理学では、ヒトには自己意識はあるがヒト以外の動物にはないと考えられてきました。ヒト以外の動物の自己意識がはじめて示されたのは、チンパンジーの鏡像自己認知が証明された1970年のことです。しかし、今でも多くの動物の自己意識は認められていません。

　今世紀に入り、単純とされてきた魚類の脳構造や神経基盤は、哺乳類の脳と相同であることがわかってきました。魚も「賢い」ことが予想され、我々は世界に先駆け魚類の賢さを、実験室で魚類を飼育し研究をしています。例えば、魚にも「A>BかつB>CならA>C」との論理的思考ができることがわかってきました。魚類がヒトや霊長類の社会に匹敵する複雑な社会を持つことはわかっています。複雑な社会での暮らしには互いの個体認識が必須であり、これなしでは社会生活はおくれません。視覚が発達したヒトや霊長類は、相手の個体ごとに異なる顔に基づき相手を識別しています。これら社会性の魚類を調べてみたら、なんと彼らもお互いの顔を認識し識別していたのです。

　魚の体表の寄生虫を食べる魚(掃除共生魚)として知られるホンソメワケベラは、縄張りと順位のある高度なハレム社会を持っています。彼らもお互いを顔で認識し(図１)、メンバー間で信頼関係を保ちながら暮らし、裏切ると罰さえうけます！2020年に、我々はこの魚が鏡に映る自分の姿をみて、自分だと認識できることを、世界で初めて発見しました(図２)。なぜ魚にこんな高度な能力があるのでしょうか？その答えは彼らの社会生活にあります。ヒトや多くの霊長類、そしてこの魚も複数の知り合いを顔で個別に識別し、各個体と個体間関係を把握しています。そこでは、他者認識だけではなく自己認識もしており、この能力が自己鏡像を自分だと認識できる基礎になっているのです。

　現在、まだヒトを頂点とする動物観が主流です。鏡像自己認知能力や自己意識など高次の認知能力はヒトや霊長類などに限られるなどと、動物の知性は大きく誤解されています。我々は魚類を対象に動物の知性や知能を今後さらに研究していきます。

地球学科

顕微メスバウアー分光法を用いた鉱物中の鉄の分析

篠田 圭司

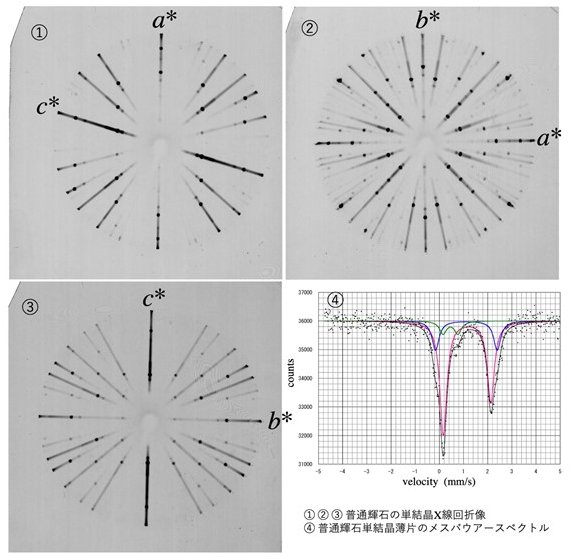
　岩石鉱物薄片試料に普遍的に存在する鉄の価数（Fe²⁺かFe³⁺か）とFe²⁺とFe³⁺の量比を、薄片状態つまり単結晶のままでの局所非破壊で分析することを目指して、半導体検出器を用いた顕微メスバウアー分光器を製作し、⁵⁷Fe顕微メスバウアー分光法に取り組んでいます。

　輝石は化学組成が(Ca, Mg, Fe)SiO₃であらわされる主要造岩鉱物です。輝石は多席固溶体で、輝石中でFeは２種類の結晶学的位置（M1席とM2席）を占めます。輝石の鉄のメスバウアースペクトルは２本（１対）のピーク（ダブレットピーク）を示します。ダブレットピークの特徴を決める４つのパラメーター（アイソマーシフト、四極子分裂幅、ピーク幅、ダブレットピーク比）は異なる席を占める鉄イオン毎にわずかに異なる値をもちます。従来、鉱物のメスバウアー分光法は、粉末状の鉱物試料で測定されてきました。粉末試料に対してはダブレットピーク比が１対１と仮定できます。一方、単結晶薄片のメスバウアースペクトルでは、ダブレットピーク比は１対１になるとは限らず、ガンマ線に対する結晶方向の違いでさまざまな値を取ります。従来のメスバウアー研究により、さまざまな鉱物の３つのメスバウアーパラメーター（アイソマーシフト、四極子分裂幅、ピーク幅）の価はよく知られていますが、単結晶試料を使った場合のダブレットピーク比の結晶方位依存性は明らかにされていません。輝石のような多席固溶体の場合、測定されたメスバウアースペクトルの解析には、生データに対してこれら４つのパラメーターで特徴づけられる最大３対のダブレットを仮定して、12のパラメーターを動かしてピーク分離して最適解を求め、各席の鉄イオンの存在比を求める必要があります。精度良く、信頼のおけるピーク分離のためには、測定している単結晶についてはダブレットピーク比がどれくらいの値を取るはずか、を知った上で生データを解析する必要があります。そこで、化学組成が単純で、鉄が１種類のM席しか占めていない輝石の定方位薄片（結晶学的方向を決めた薄片）を作成し、結晶軸に対するガンマ線の入射方向に対してダブレットピーク比が計算できるテンソル量を実験的に決める研究に取り組んでいます。定方位薄片の作成と作成した薄片内での結晶軸の決定にはX線回折法を用いています。数種類の固溶体組成の異なる輝石の定方位薄片を用いた単結晶メスバウアースペクトルの測定から、ダブレットピーク比を決めるテンソル量の固溶体組成依存性を明らかにしつつあります。